ejercicios de circunferencia y circulo 2

Dos circunferencias de radio 10 metros tienen sus centros a 16 metros de distancia de tal forma que las dos circunferencias se interceptan. ¿cual es el área de su intersección?

Modelo del problema

para resolver este problema ubiquemos dos triángulos isósceles o cuatro rectángulos. 

se observan 2 triángulos isósceles: el Triangulo ACR y el Triangulo ABR, estos dos triangulos son congruentes dado que ambos comparten el segmento AR y y los segmentos AC, CR, AB y BR son congruentes entre si por ser los 4 radios de las circunferencias y en las dos circunferencias el radio es de 10 m. ademas de ser congruentes los dos triángulos son isósceles.

cada triangulo isósceles se puede descomponer en dos triángulos rectángulos. que serian congruentes entre si, el ACG, elABG, el RBG y el RCG.

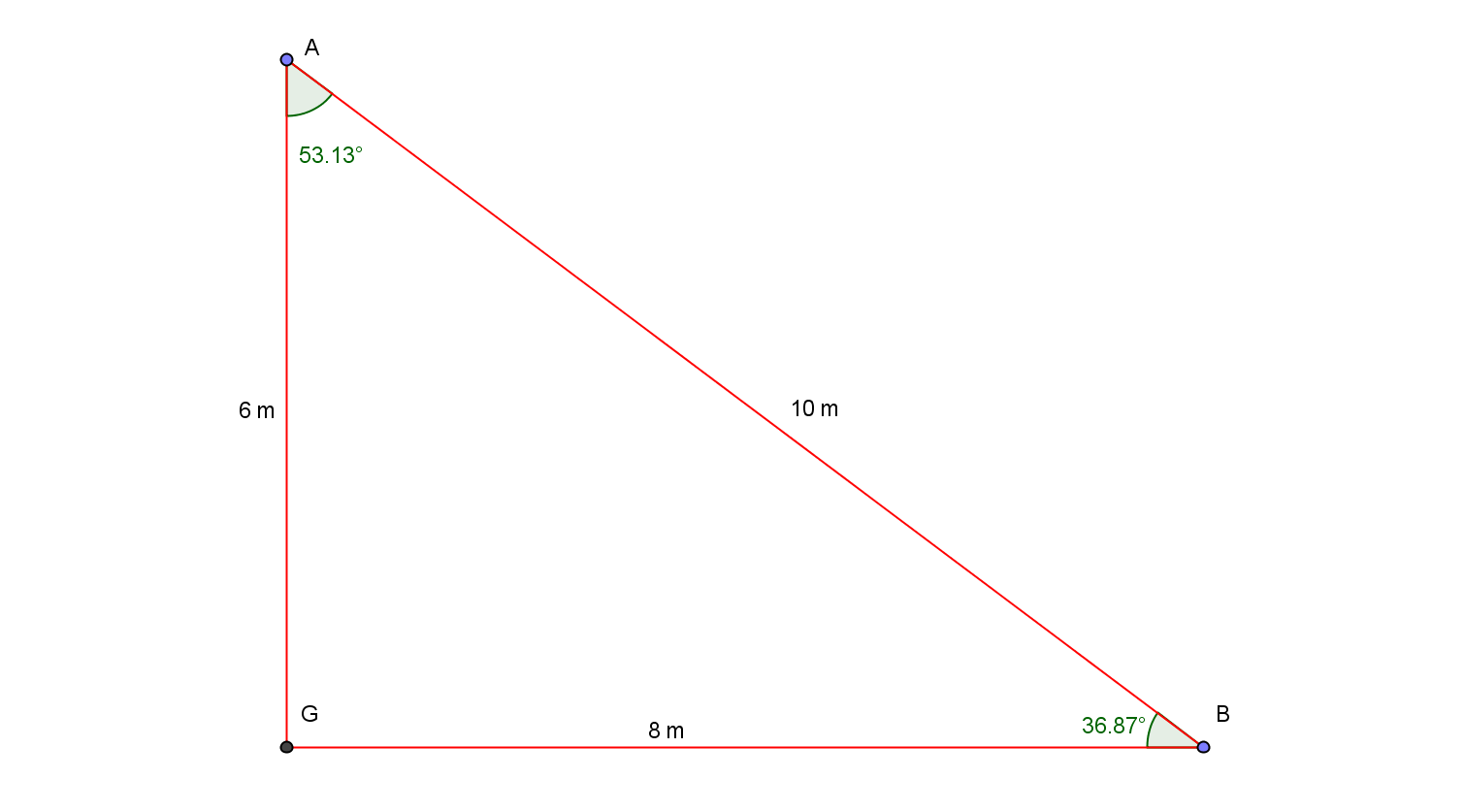
Uno de los triángulos rectángulos es como el que se muestra abajo 

aplicando el teorema de Pitágoras podemos determinar la medida del segmento GA

Observa ahora que este triangulo es un Triangulo semejante al Triangulo sagrado de Isis, o Triangulo Egipcio o triangulo 3-4-5, si lo hubiéremos notado anteriormente no hubiera sido necesario realizar el calculo de Pitágoras para determinar el lado faltante.

Dado que el punto G es el punto medio del segmento AR, podemos asegurar que la medida de AR es 12 m.

podemos calcular ahora la medida del angulo ABG.

y dado que el angulo GAB es complementario con el ABG, entonces el angulo GAB mide 53.13 grados.

Como el triangulo ABG se obtuvo de dividir el triangulo ABR en un eje de simetría podemos establecer que la medida del angulo ABR es el doble de la medida del angulo ABG, por tanto el Angulo ABR mide 73.74 grados, la cual también es la medida del angulo ACR  dado que los triángulos isósceles ACR y ABR son congruentes.

Para calcula el área del Triangulo ABR, nos guiaremos ahora por la siguiente figura:

el triangulo de la figura que es uno de los dos triángulos isósceles que se forman en las dos circunferencias tiene por altura el segmento AG si consideramos que la base es AR por tanto el área de este triangulo es 

tenemos que el triangulo al cual le calculamos su area esta dentro de el sector circular que mostramos abajo.

para calcular el área del sector requerimos transformar la medida del angulo a radianes

el área del sector esta dada entonces por

:

Tenemos entonces lo siguiente:

y el triangulo isósceles que se forma por los radios queda así:

por diferencia podemos calcular que el área del sector circular que no forma parte del triangulo mide 16.35 m2.

dado que las dos circunferencias son congruentes y a que existe simetría en el trazo, podemos concluir que el área de intersección de las dos circunferencias es el doble de 16.35 m2. como lo mostramos en la figura siguiente:

ejercicios circunferencia y circulo

desarrollaremos algunos problemas típicos de este tema:

Un auto en una pista circular recorre un ángulo de 135^o y barre un longitud de arco de 54π metros.

1. Hallar el radio de la pista circular.
2. Hallar el área del sector circular recorrida.

modelo del problema:

la circunferencia mostrada tiene radio r y sabemos que la longitud que recorre un automóvil es 

sabemos ademas que en un sector circular se cumple que:

dado que conocemos S, y el angulo podemos despejar el valor de r 

para poder usar esta expresión debemos de transformar el ángulo a radianes, esto es cambiar la medida del angulo en grados a la medida que tendría un arco de una circunferencia unitaria si fuese generado por un angulo de 135 grados.

sabemos que una circunferencia unitaria tiene una circunferencia que mediría 2 veces Pi, por lo que es valida la siguiente proporción:

De esta proporción se puede hacer el desarrollo siguiente:

ahora es posible que obtengamos el radio de la curva que recorre el auto del problema:

de lo anterior podemos concluir que el radio de la curva que toma el auto es de 72 metros.

El Área del sector circular generado por la curva en estudio será:

Teorema del triangulo isósceles

Un triangulo isósceles es aquel que tiene dos lados de igual magnitud.

El teorema del Triangulo isósceles se enuncia de la siguiente forma:

"Si dos lados de un triangulo son congruentes, entonces los ángulos opuestos son congruentes también".

Antes de probar lo anterior expliquemos de que habla este Teorema

En primer lugar se habla de lados congruentes, en geometría decimos que dos cosas son congruentes cuando tienen la misma forma y magnitud, en el triangulo isósceles de la figura vemos que esta compuesto por tres segmentos el AC, el CD y el DA, si el triangulo es isósceles entonces AC = AD y por tanto son congruentes.

Sabemos ademas que cualquier triangulo tiene tres ángulos internos:

En este triangulo los angulos internos son <DCB, <CAD y <ADC.

vemos que enfrente de cada angulo hay un lado del triangulo, por ejemplo el <ADC es opuesto al lado CA.

Cada lado del triangulo tiene un angulo opuesto.

lo que el Teorema del triangulo isósceles establece es que dado que lo segmentos AC y ad son congruentes, los <ACD y <ADC deben de ser congruentes tambien.

procedemos a probar esta afirmación, para lo cual añadiremos un trazo mas a la figura.

Si el triangulo Mostrado es isósceles entonces el segmento AD y el segmento AC son congruentes, en el segmento CD que es el que no es congruente ubicamos su punto medio al cual llamamos E y trazamos un segmento de recta que une este punto con el vértice A.

Nos damos cuenta que hemos dividido el triangulo ACD en dos triangulos: el triangulo ACE y el triangulo ADE.

comparamos los dos triangulos y observamos lo siguiente:

I) el segmento AC y el segmento AD son congruentes por ser nuestro supuesto de partida.

II) el segmento CE y el segmento ED son congruentes ya que el punto E es el punto medio del segmento CD y por tanto cada uno de estos subsegmentos es la mitad del mayor y por tanto son congruentes.

III)el segmento AE es compartido por los dos triangulos y debe de ser congruente consigo mismo.

conclusión:

Dado que los dos triángulos tienen lados congruentes una a uno entonces decimos que los triángulos son congruentes.

Si dos Triángulos son congruentes es porque tienen la misma forma y dimensiones, por lo que los ángulos deben de ser congruentes.

Por tanto el <ACE, que es el mismo que el <ACD es congruente con el <ADE que es el mismo que el <ADE.

Dado un segmento de recta, encontrar su punto medio

División de un segmento de recta en dos partes iguales.

Un primer problema que enfrentaron los Griegos, fue como dividir un segmento de recta exactamente en dos partes iguales, Griegos y romanos no tuvieron una adecuada manera de representar los números, lo que les impidió hacer mayores progresos en el cálculo matemático, sin embargo con ayuda de los razonamientos geométricos pudieron realizar operaciones tales como la división de un segmento.

El planteamiento del problema es el siguiente:

Dado un segmento cualquiera, encontrar el punto que lo divide exactamente en dos partes iguales:

primer paso: trazar dos circunferencias, una con centro en A y otra con centro en B con el mismo radio que claramente sea mayor que la mitad del segmento.

notemos que las dos circunferencias se interceptan en dos puntos, llamemosles D y E

segundo paso: Únanse los puntos E y D con un segmento de recta. 

el Punto de intersección  del Segmento AB con el segmento DE al que llamamos F es el punto medio del segmento AB y del Segmento ED.

El procedimiento indicado es muy simple, pero si aplicamos el rigor matemático a la prueba antes realizada, nos queda la duda de si esto siempre se cumple, es necesario demostrar que con este procedimiento siempre se obtendrá el punto medio de un Segmento.

prueba

 A la última figura la añadiremos 4 segmentos más: AD, BD, AE y BE

I) Observamos que se han formado 4 Triángulos: ADF, AEF, BDF y BEF.

II) Los segmentos AD, BD, AE y BE miden lo mismo por ser radios de circunferencias de igual radio.

III) Sabemos que el <AFD y el <DFB suman dos angulos rectos, es decir son suplementarios.

IV) De igual forma el <AFE y el <EFB también son suplementarios.

V) De la misma forma el <AFB y el <BFD también son suplementarios.

VI) De igual forma son suplementarios <AFD y >AFE.

VII) Sabemos además que dos ángulos opuestos por el vértice son congruentes, esto quiere decir que miden lo mismo. por tanto los <AFD y <BFE son congruentes de la misma manera que <AFE y <BFD.

IX) si observamos los Triángulos BFD y AFD, nos damos cuenta que ambos tienen en común el segmento FD.

X) la única forma en la cual AD y DB sean iguales en los triángulos FDB y FDA es que <AFD y <BFD sean congruentes.

XI) la única forma de que <AFD y <BFD sean congruentes dado que suman dos ángulos rectos es que cada uno de ellos sea un ángulo recto.

XII) por lo tanto <AFD , <BFD,<AFE y <EFB son congruentes e iguales a un ángulo recto.

XIII) el triangulo que tiene un angulo recto como angulo interior se le conoce como Triángulo rectángulo, por tanto los triángulos ADF, AEF, BDF y BEF son rectángulos.

XIV) Si en dos triángulo rectángulo conocemos la hipotenusa y un cateto y estos son iguales, entonces el cateto restante debe de ser igual. (esto se demostrara posteriormente) por tanto los segmentos FB y FA deben de ser iguales y como ambos suman el segmento AB, entonces f debe de ser el punto medio de ese segmento.

Teorema del Angulo Externo

¿Que es un Teorema?

Un teorema es una proposición que afirma una verdad demostrable. En matemáticas, es toda proposición que partiendo de un supuesto (hipótesis), afirma una verdad (tesis) no evidente por sí misma

En el curso de Trigonometría de la escuela preparatoria se presentaran varios teoremas, un teorema no es una verdad que se acepta ciegamente, siempre debe de ser probada la veracidad de su afirmación.

Expondré en primer lugar un teorema que se le atribuye a Euclides la demostración ya que aparece en el libro I del ya citado "Los Elementos".  Lo mas probable es que este Teorema venga desde un periodo muy anterior al padre de la Geometría, sin embargo, la primera cita que tenemos del mismo es precisamente en el libro que comentamos.

Teorema: Si se considera cualquiera de los ángulos exteriores a un Triangulo ABC, entonces su medida es mayor que la de cualquiera de los ángulos interiores no adyacentes a el.

Antes de demostrar este teorema pongamonos de acuerdo en un lenguaje que será utilizado a lo largo de este Blogg.

En primer Lugar el enunciado del Teorema que estudiamos habla de un Triangulo ABC.


Un Triangulo, como es bien sabido es una figura geométrica compuesta por tres lados y por tres ángulos, los lados de un triangulo son segmentos de recta, los cuales se interceptan en tres puntos que son llamados vertices.

El triangulo de la imagen tiene vertices en el punto A, el punto B y el Punto C. Esta delimitado por el segmento AB, el Segmento CB y el  Segmento CA.

Podemos intuir que lo que define en primera instancia al triangulo son precisamente los tres puntos A, B y C, de hecho esto es un Teorema que será demostrado más adelante, una vez que contemos con los elementos matemáticos para hacerlo. Debido a esta observación para hablar del triangulo en cuestión lo haremos refiriéndonos a el como el Triangulo ABC, aunque también podríamos hablar de el como el Triangulo BCA o como el Triangulo CAB, en cualquiera de los tres casos estaríamos hablando del mismo triangulo.

El Teorema que estudiamos no habla directamente del Triangulo ABC, mas bien habla de los ángulos exteriores al Triangulo ABC.

En la figura de arriba tomamos el triangulo que analizamos y utilizando el segundo postulado de Euclides prolongamos el segmento AC hacia el punto D. Observamos que al hacer esto quedan claramente marcados dos ángulos con vértice en el punto C. Se observa el angulo nombrado como beta el cual es un angulo interior del Triangulo ABC, para referirnos a este angulo lo nombraremos <ACB ó <BCA, esto significa que nos referimos al angulo que inicia su trazo en el punto A, tiene un vértice en el punto B y concluye su trazo en el punto C. observamos que en este triangulo tenemos otros dos angulos internos, a saber el <ABC y el <CAB.

se observa un  segundo ángulo al cual nombramos alfa en la figura, este es un angulo externo y para referirnos a el decimos que es el <DCB ó <BCD.

pregunta:

¿cuantos ángulos externos podemos dibujar en cualquier triangulo?

entregar mañana en clase un dibujo en hoja tamaño carta con los otros trazos posibles para un angulo externo de un Triangulo ABC.

Decimos que el <ACB es adyacente al < BCD, los otros dos ángulos internos del Triangulo ABC  son ángulos no adyacentes al <BCD.

Entonces para probar el teorema enunciado al principio de esta entrada es necesario demostrar que <BCD es mayor que el <BAC y que es mayor que <ABC.

Primer paso. probar que <DCB es mayor que <ABC.

a) consideremos el triangulo que hemos estado construyendo. encontremos el punto medio del segmento BC

a este punto que encontramos lo llamaremos E, solo consideraremos por el momento el <BCD, que ahora también lo podemos llamar <ECD y se encuentra marcado en la figura como alfa, aunque en el siguiente paso eliminaremos estas notación.

b) unamos con un segmento de recta el punto E y el punto A

el segmento AE que hemos trazado se le conoce como Mediana del triangulo sobre la base CB

c) Trazamos una circunferencia con centro en E y radio EA.

d) prolongamos el segmento AE por E para formar una semirrecta y encontrar el punto F que es la intersección de la semirrecta con la circunferencia por el lado de E.

observemos que la medida del segmento EF debe de ser igual a la medida del segmento AE, por ser ambos radio de la misma circunferencia.

e) Unamos el punto C con el Punto F.

Razonamiento.

I) El <BEA mide lo mismo que el <FEC, por estar opuesto por el vértice.
II) El segmento BE mide lo mismo que el segmento EC por ser E el punto medio del segmento BC.
III) El segmento AE mide lo mismo que el segmento EF por ser ambos radios de una circunferencia.

IV) Por lo anterior podemos concluir por el postulado LAL que los triángulos ABE y FCE son congruentes.
V) Dado que los triángulos son congruentes el angulo ABC y el angulo FCE miden lo mismo.
VI) El <FCE es parte del  <DCB.
VII)  Dado que el todo debe ser mayor que la parte, entonces concluimos que el <DCB que es externo al Triangulo ABC en el vértice C es mayor que el  <ABC, que es uno de los ángulos no adyacentes al <DCB.



tarea para entregar: probar que el <BAC es menor que el <DCB

Axiomas y Postulados de Euclides

Defiende tu derecho a pensar, porque incluso pensar de manera errónea es mejor que no pensar. 

Hipatia de Éfeso, 370-415 dJC 

Pensadora vinculada a la Biblioteca de Alejandría

Euclides de Alejandría (-325aC- -265aC) fue uno de los jóvenes discípulos de Platón. No se conservan demasiados datos sobre su vida. Por ejemplo no nos consta su lugar de nacimiento. A menudo se confunde con Euclides de Megara, discípulo de Sócrates. Fue coetáneo del instaurador de la dinastía tolemaica Tolome Sóter, después, por tanto, de la muerte de Alejandro Magno. Creó escuela y enseñó en Alejandría.

Se cree también que Euclides no hacía énfasis en los aspectos prácticos de la materia. Se cuenta que en una ocasión uno de sus alumnos le preguntó qué utilidad tenía estudiar geometría. Euclides ordenó a uno de sus esclavos que le diese unas monedas, ya que debe ganar algo necesariamente de lo que aprende. 

Su gran obra es una colección de libros llamados "Los Elementos", dividido en 13 volúmenes, en los cuales se recopilan las matemáticas de entonces. La estructura de estos libros consiste en un pórtico axiomático donde se encuentran las definiciones, postulados y nociones comunes. 

Son las reglas del juego a partir de las que se deducen las proposiciones. Es la primera vez en la historia que se abordan las matemáticas desde esta perspectiva. 

En mi opinión, desde la perspectiva del curso de Trigonometría de la escuela preparatoria de La Universidad Autónoma del Estado de México lo mas valioso que aporta la obra de Euclides es la sistematización de la construcción del conocimiento matemático, bajo un método que posteriormente fue trasladado a otros campos del saber.

La obra "Los Elementos", de la cual se ha tomado la ilustración que se muestra en la parte superior, precisamente en la proposición que demuestra el teorema de Pitagoras, esta dividida en 13 Libros.

Iniciaremos la exposición de este curso partiendo del estudio del Libro I de "los Elementos de Euclides". En este primer libro se plantean cinco postulados, 9 axiomas, 23 definiciones y 48 proposiciones que dejan las bases de la construcción de la Geometria Griega.

No perdamos de vista que los Griegos no conocían el Álgebra y su sistema de numeración no se prestaba para el uso de la Aritmética, por lo que la geometría se convirtió en algo mucho mas importante que una técnica de dibujo. 

Los 9 Axiomas de Euclides

Antes de enunciar los Axiomas que sirven de base para el pensamiento matemático, definamos lo que es un Axioma

Un axioma es una proposición que se considera «evidente» y se acepta sin requerir demostración previa. En un sistema hipotético-deductivo es toda proposición no deducida (de otras), sino que constituye una regla general de pensamiento lógico 

Partiendo de lo anterior, Euclides acepto la existencia de los siguientes Axiomas:

1. Cosas iguales a una misma cosa son iguales entre si.
2. Si a cosas iguales se agregan cosas iguales, los totales son iguales.
3. Si de cosas iguales se quitan cosas iguales, los restos son iguales.
4. Si a cosas desiguales se agregan cosas iguales, los totales son desiguales.
5. Las cosas dobles de una misma cosa son iguales entre si.
6. Las cosas mitades de una misma cosa son iguales entre si.
7. Las cosas que son congruentes entre si, son iguales entre si.
8. El todo es mayor que la parte.
9. Dos rectas no comparten espacio.

Es claro que las 9 propuestas anteriores son tan evidentes que no se requiere ninguna demostración al respecto.

Los 5 postulados de Euclides.

Un postulado es una proposición no evidente por sí misma, ni demostrada, pero que se acepta ya que no existe otro principio del que pueda ser deducida

Primer postulado de Euclides.

"Una recta puede trazarse desde un punto cualquiera hasta otro punto cualquiera":

Segundo postulado de Euclides:

"Un segmento de recta puede prolongarse por cualquiera de sus extremos, convirtiéndose en una recta".

Tercer postulado de Euclides:

"Una Circunferencia puede describirse con un centro y una distancia".

Cuarto Postulado de Euclides:

"Todos los Ángulos rectos son iguales entre si"

Quinto Postulado de Euclides:

"Si una recta corta a otras dos, forma con estas dos ángulos interiores cuya suma es menor que la suma de dos ángulos rectos, si las dos rectas cortadas se prolongan indefinidamente, se interseptaran del lado que la suma de los ángulos interiores en menor que dos ángulos rectos"